Si vous avez été amenés à aider un enfant à calculer des divisions, vous vous êtes sans doute heurtés à une manière de les poser qui vous a surpris et qui a pu vous paraître à la fois lente et confuse. Qu’en est-il réellement ?
- Une manière plus lente : oui, vous avez raison car on laisse une trace écrite de toutes les étapes de l’opération
- Une manière plus confuse : non, là, vous vous trompez c’est au contraire plus clair pour les élèves car bien plus explicite.
Comment procède-t-on ?
Je vous propose deux étapes :
- La division avec un diviseur à 1 chiffre
- La division avec un diviseur à 2 chiffres
Une remarque en passant :
Les divisions du type 32 458 divisé par 783 qui ont assombri les matinées de classe des plus vieux d’entre nous n’ont heureusement plus cours dans les classes aujourd’hui.
Il s’agissait d’un exercice fastidieux qui ne correspondait à aucune situation mathématique que des enfants pouvaient rencontrer dans la vie réelle. On ne partage pas par un nombre de plus de 2 chiffres, on fait une estimation. Dans les problèmes de CM2 on était obligé de passer par des ficelles un peu grosses, par exemple : trouver la largeur d’un champ dont on donnait l’aire, ici 32 458m² et la longueur, ici 783m.
Ceci est terminé et on ne peut que s’en féliciter.
Restent les divisions par un diviseur à 1 puis, pour les plus grands à 2 chiffres qui mettent encore bien des élèves en difficulté.
I.La division avec un diviseur à un chiffre
Un exemple : 165 divisé par 7.
A. Avec l’ancienne méthode.
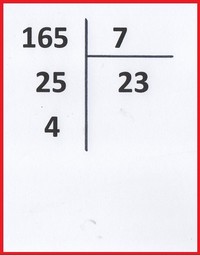
J’écris en italiques ce que l’on dit :
En 16, combien de fois 7 ? 2 fois 7 =14; 14 allé à (ou ôté de) 16, il reste 2.
J’abaisse le 5. En 25 combien de fois 7 ? 3 fois 7=21. 21 ôté de 25, il reste 4
B. Avec la méthode actuelle.

J’ai changé de couleur pour le chiffre des unités pour faciliter la lisibilité.
On procède de la même manière, simplement on pose les soustractions.
En 16, combien de fois 7 ? 2 fois 7 =14; j’écris 14 sous 16.Je calcule la soustraction. 6 moins 4 il reste 2, 1 moins 1, il reste 0 (on l’écrit ou non).
J’abaisse le 5. En 25 combien de fois 7 ? 3 fois 7=21. J’écris 21 sous 25. Je calcule la soustraction. 5 moins 1, il reste 4, 2 moins 2, il reste 0.
II.La division avec un diviseur à 2 chiffres
Un exemple : 5731 divisé par 21
A. Avec l’ancienne méthode.
Il y a 2  chiffres au diviseur, j’en prends 2 au dividende.
chiffres au diviseur, j’en prends 2 au dividende.
En 57 combien de fois 21 ? 2 fois. 2 fois 1 = 2. 7 moins 2 = 5; 2 fois 2 =4; 5 moins 4 =1.
J’abaisse le 3. En 153, combien de fois 21? 7 fois. 7 fois 1 = 7; 3 moins 7, je ne peux pas donc 13 moins 7 =6. 7 fois 2 = 14 plus 1 de retenue =15. 15 moins 15 = 0
J’abaisse le 1. En 61, combien de fois 21? 2 fois. 2 fois 1 = 2; 1 moins 2, je ne peux pas donc 11 moins 2 =9. 2 fois 2 = 4 plus 1 de retenue =5. 6 moins 5 = 1.
B. Avec la méthode actuelle.

Même remarque que tout à l’heure : on procède de manière identique mais on pose chaque fois les soustractions.
Il y a 2 chiffres au diviseur, j’en prends 2 au dividende.
En 57 combien de fois 21 ? 2 fois. 2 fois 1 = 2, j’écris le 2 sous le 7. 2 fois 2 =4, j’écris le 4 sous le 5. Je calcule la soustraction. 57 moins 42= 15.
J’abaisse le 3. En 153, combien de fois 21 ? 7 fois. 7 fois 1 = 7, j’écris le 7 sous le 3. 7 fois 2 = 14, j’écris le 14 sous le 15. Je calcule la soustraction 153 moins 147 = 6
J’abaisse le 1. En 61, combien de fois 21? 2 fois. 2 fois 1 = 2, j’écris le 2 sous le 1. 2 fois 2 = 4, j’écris le 4 sous le 6. Je calcule la soustraction. 61 moins 42 =19.
Vous avez tout à fait le droit de préférer votre bonne vieille méthode de calcul mais il serait imprudent de tenter de l’expliquer à votre enfant et, a fortiori, de la lui imposer et ce pour plusieurs raisons.
- Vous risquez d’engendrer chez lui de la confusion car un élève de cycle 3 a rarement assez de recul pour comprendre qu’avec la méthode ancienne on effectue la même opération sans la poser
- La méthode actuelle est mieux adaptée aux enfants d’aujourd’hui qui sont bien moins habitués au calcul mental que ne l’étaient leurs grands-parents au même âge. Beaucoup d’élèves se perdent dans leurs calculs s’ils n’écrivent pas tout.
- La division, surtout lorsqu’on a un diviseur à 2 chiffres, est une opération difficile qui exige souvent des phases de tâtonnement, particulièrement lorsque le chiffre des unités du diviseur est supérieur à 5. Dans l’exemple ci-dessus, s’il avait fallu diviser par 29 et non par 21, l’élève aurait très probablement proposé 2 pour se rendre compte ensuite que c’était trop fort.
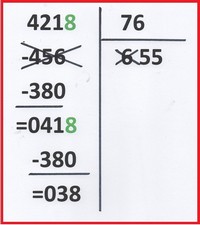
Or, lorsqu’il y a tâtonnement, (image ci-contre) il s’avère plus facile pour les élèves d’écrire la soustraction puis de la barrer (pas de l’effacer!) et de recommencer avec un nombre inférieur pour le quotient.
Sans doute est-ce moins joli sur le cahier mais au moins l’élève voit où il en est et ce qu’il fait; et…
… c’est bien l’essentiel car, s’il s’agit seulement de trouver un résultat, nos enfants ne sont pas fous, ils savent bien qu’existent les calculettes !